This blog is a new series on exploits in poker using mass data analysis (MDA) and counter factual regret minimization. I plan to use the posts as a way to track my investigations into new spots and hopefully introduce some new ideas into the community. This first post requires almost no knowledge of poker beyond the rules of the game and some definitions I provide below. We will focus on microstakes (Max buy-in of 5$) 6-max poker using anonymous based sites (Ignition/Bovada for example) to investigate exploits solely at the population level.
Useful Definitions:
- 6-max poker has 6 positions. We will commonly refer to these via name throughout the series. They are visualized by the following table:
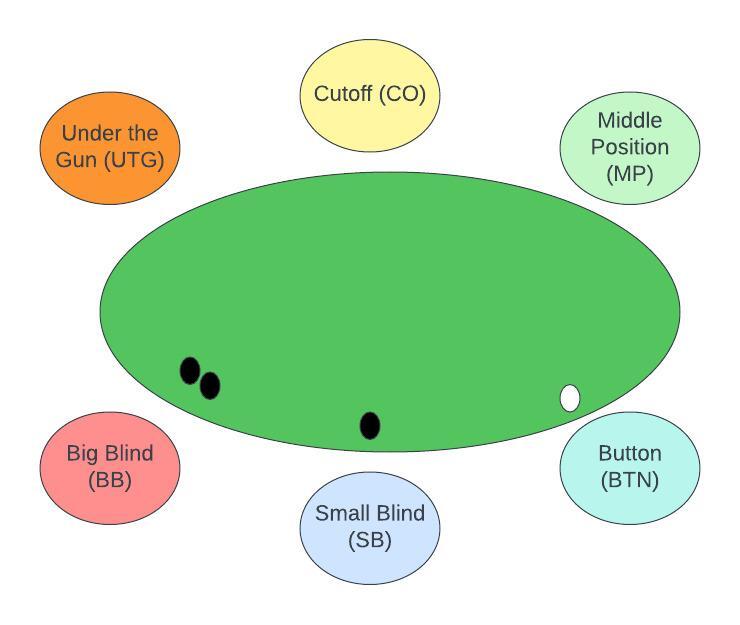
- The small blind is the worst position since it is the first to act postflop . The button is the best position since it is the last to act. (Actions follow a clockwise direction)
- Preflop, note that the UTG player will act first and BB is last to act. (Same clockwise direction)
- Expected value: Poker has randomness (due to what card is next to come). Expected value is the average payout or net worth of choosing a specific action if you were to randomly simulate the game millions of times. It is a good way to measure if your action is good or bad compared to another action.
- Counterfactual regret minimization (CFRM): An algorithm that allows us to find the EV of any action given that our opponent also plays
perfectly
(meaning they chose the action with highest EV all the time) - Game theory optimal(GTO): We refer to the GTO action as the one chosen by counterfactual regrent minimization or the
solver
. - Exploits: When our opponent does not play perfectly (not GTO), how can we punish them? These are called exploits.
Preflop Exploits:
In this first post, we will start with the simplest possible exploit at the earliest action - preflop. In particular, we will look at spots where everyone has folded except for the small and big blinds. Now, what questions are worth asking in this spot? Three important ideas come to mind.
- What is the
correct
or GTO action for the small and big blinds? - What is our population doing in the big blind at a mass level? Is this correct?
- If incorrect, how can we exploit this action?
Naturally, let us answer the first question. Using an implementation of CFRM and a 5% rake structure with 5 Blind(B) cap (Rake: each hand, the casino will take 5% of the pot with a maximum of 5 blinds). I have developed a simplified (no limping) simulation of a blind versus blind secnario.
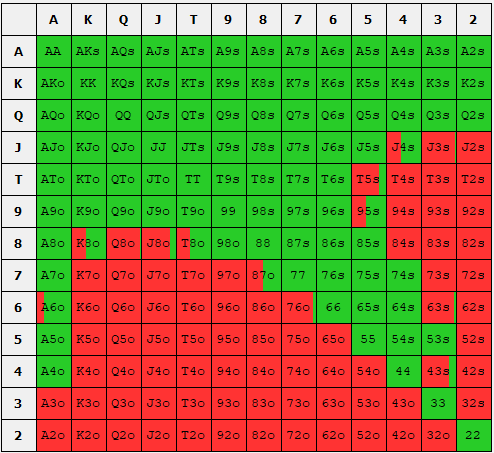
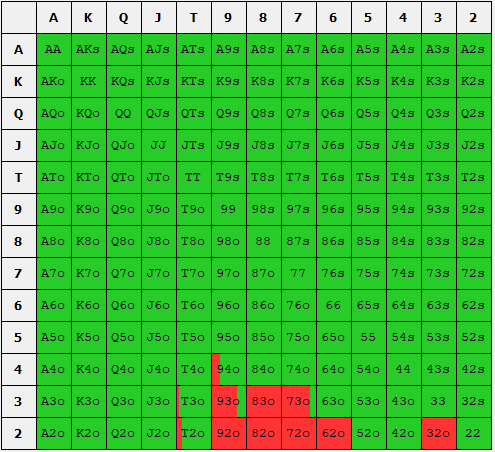
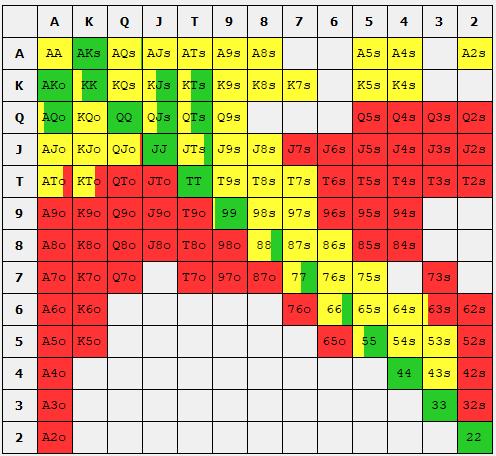
GTO simulation of the SB opening range (left) and the BB defend range (right). SB raises to 3B and BB can reraise to 9B. Green indicates a raise. Yellow indicates a call. Red indicates a fold.
We can see in the above figure that the SB should open around 43% of hands to 3B and the BB should call (indicated in yellow) or defend
approximately 34% of the time. Additionally, the BB should raise (indicated in green) to 9B approximately 20% of the time. The set of hands that the SB should raise is called the SB raising range and likewise the set of hands the BB should defend is called the BB defense range. Generally, the word range means the set of hands that one should take a particular action with.
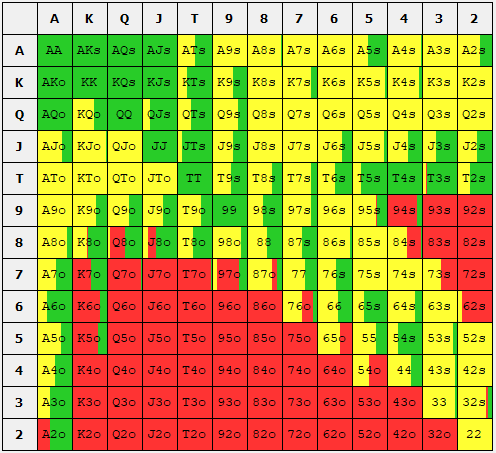
Ok, now that we see what the BB should be doing in defense of a SB raise, let us ask the question: What is the population doing? Over 100k hands, I have calculated exactly the ratios that the BB is defending, raising, and folding when facing a 3BB SB raise. I present these below and the exact values are the BB is raising 11.27% of their hands, calling 35.13% of their hands, and folding 54.6% of their hands.
BB defense range for 100k dataset of populations hands. Green indicates a raise. Yellow indicates a call. Red indicates a fold.
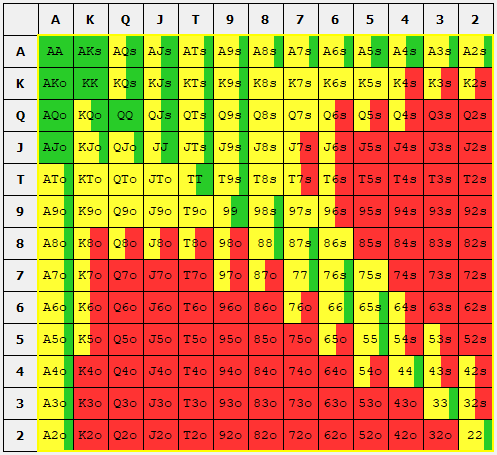
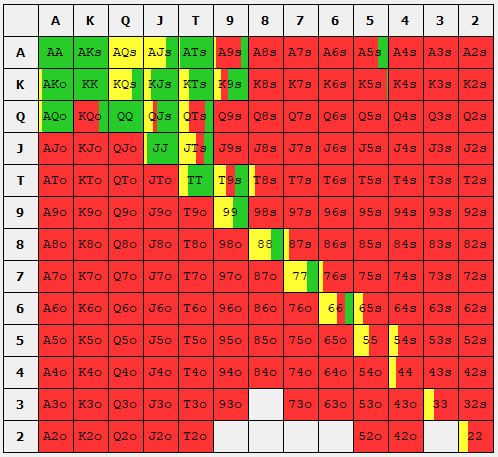
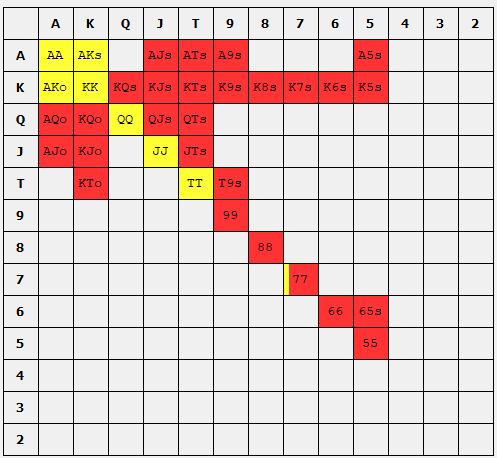
So, onto the third question: How to exploit them? In the CFRM algorithm, I forced the BB to act in accordance with the figure above and calculated the response. Below, I present the results (left) compared with the original GTO solution from above (right).

GTO simulation of the exploitative SB opening range (left) and the GTO range (right). Green indicates a raise. Red indicates a fold.
We can see that the SB now opens a whopping 92.56% of hands! By this numerical result, the CFRM algorithm is telling us that the BB is not effectively defending enough of their hands and so we should over-open our hands with the assumption that the BB will fold too often. Naturally one might ask how the expected value of each action changes? I present the EV values below.
| Fold | Call | SB Raise/BB Reraise | |
|---|---|---|---|
| GTO Small Blind EV | -5 | N/A | 68.113 |
| Exploited Small Blind EV | -5 | N/A | 47.462 |
| GTO Big Blind EV | -10 | 76.89 | 138.86 |
| Exploited Big Blind EV | -10 | 60.553 | 57.91 |
We can see that although in the exploitative case, both the BB and SB EV is lower, the raising EV for the BB is detrimentally diminished by the population's poor strategy. This indicates to us that the larger issue with the population's strategy is thier choice of raising hands.
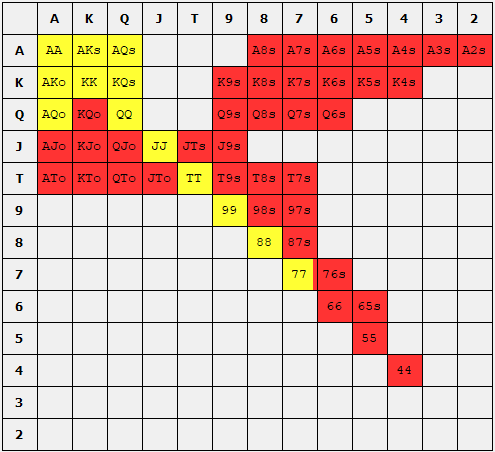
So far, we have only looked at one spot - the BB defense with a SB 3B open. It is reasonable to now ask ourselves, what should the SB do if the BB raises to 9BB? Again, I have calculated the optimal strategy and present it below.
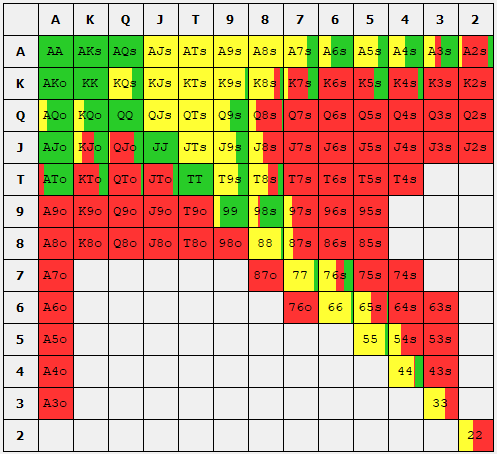
Comparison of SB defense range when facing a 3-Bet from the BB between exploitative solution and GTO solution using a nodelocked BB defense range as presented above. Green indicates a raise. Red indicates a fold.
We see that of the hands the small blind raises initially, it will reraise 22.92%, call 21.33%, and fold 55.95% of hands. However, when the SB changes its strategy to exploit the BB by opening 92% of hands, the response to the BB reraise is equally as exaggerated as the SB now folds 88% of their hands in which they originally opened! Additionally, we can see that the EV is slightly larger for the hands the SB chooses to coninue with compared to the GTO Solution!
| Fold | Call | SB Jam | |
|---|---|---|---|
| GTO Small Blind EV vs BB 3Bet | -30 | 214.409 | 277.336 |
| Exploited Small Blind EV vs BB 3Bet | -30 | 251.73 | 285.045 |
From these results, we see that going down the path where the BB choses to raise the exploiting SB, we can see that the SB's exploitative strategy generates larger EV compared to the GTO solution. This thought process of exploitation can be continued throughout the entire street of raising and reraising between the small and big blinds. For the reader's interest, I present the resulting ranges through all potentially streets after the conclusion below.
In this first post, I highlighted exactly how poker exploits work from a mass data and solver point of view. I showed the simplest example for a SB and BB preflop battle. This post serves as a first glimpse into the world I have been spending many hours studying over the past few months. In future posts, I plan to extend this work into looking at BTN opening exploits against weak SB and BB players. Furthermore, for simplicity, a counter analysis of how the SB can then be exploited due to playing an exploitative strategy themselves is omitted, but it is an important question I would ask the reader to think about. How does this counter exploitation continue back and forth and does it stop? (This is exactly how CFRM works) If you got this far into the blog post, I appreciate you reading and feel free to send me an email if you have any comments or changes: lbhan@ucsd.edu.
SB Opening Range (3BB)





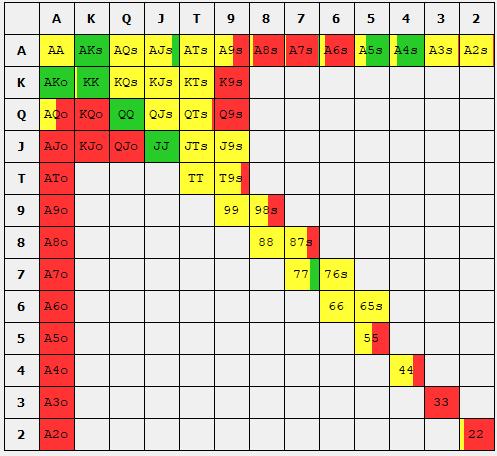
Comparison of entire game tree between exploitative solution and GTO SB solution. Green indicates a raise. Red indicates a fold.